Electronics & Communication Gate Yearwise
Electronics and Communication GATE 2024 Questions with Answer
Ques 1 Communication Systems
A digital communication system transmits through a noiseless bandlimited channel [-W W].
The received signal $z(t)$ at the output of the receiving filter is given by $z(t)=\sum_{n}b[n]x(t-nT)$ where $b[n]$ are the symbols and $x(t)$ is the overall system response to a single symbol.
The received signal is sampled at $t=mT$. The Fourier transform of $x(t)$ is $X(f)$.
The Nyquist condition that $X(f)$ must satisfy for zero intersymbol interference at the receiver is
Ques 2 Communication Systems
A white Gaussian noise $w(t)$ with zero mean and power spectral density $\frac{N_{0}}{2}$ when applied to a first-order RC low pass filter produces an output $n(t)$.
At a particular time $t=t_{k}$ the variance of the random variable $n(t_{k})$ is
Ques 3 Communication Systems
An amplitude modulator has output (in Volts)
s(t) = A cos(400πt) + B cos(360πt) + B cos(440πt).
The carrier power normalized to 1Ω resistance is 50 Watts.
The ratio of the total sideband power to the total power is 1/9.
The value of B (in Volts, rounded off to two decimal places) is
1 is the correct answer.
Ques 4 Communication Systems
A source transmits a symbol s, taken from {-4, 0, 4} with equal probability, over an additive white Gaussian noise channel.
The received noisy symbol r is given by r = s + w where the noise w is zero mean with variance 4 and is independent of s.
Using $Q(x) = \frac{1}{√2π} ∫_x^∞ e^{-\frac{t^2}{2}} dt$, the optimum symbol error probability is
Ques 5 Communication Systems
The information bit sequence {111010101} is to be transmitted by encoding with Cyclic Redundancy Check 4 (CRC-4) code, for which the generator polynomial is C(x) = x4 + x + 1.
The encoded sequence of bits is
Ques 6 Communication Systems
Let X(t) = A cos(2πf0t + θ) be a random process, where amplitude A and phase θ are independent of each other, and are uniformly distributed in the intervals [-2, 2] and [0, 2π], respectively.
X(t) is fed to an 8-bit uniform mid-rise type quantizer.
Given that the autocorrelation of X(t) is $R_x(τ) = \frac{2}{3} cos(2πf_0 τ)$, the signal to quantization noise ratio (in dB, rounded off to two decimal places) at the output of the quantizer is
45.84 is the correct answer.
Ques 7 Computer Organization
A machine has a 32-bit architecture with 1-word long instructions.
It has 24 registers and supports an instruction set of size 40. Each instruction has five distinct fields, namely opcode, two source register identifiers, one destination register identifier, and an immediate value.
Assuming that the immediate operand is an unsigned integer, its maximum value is
16383 is the correct answer.
Ques 8 Control Systems
In the context of Bode magnitude plots, 40 dB/decade is the same as
Ques 9 Control Systems
In the feedback control system shown in the figure below $G(s)=\frac{6}{s(s+1)(s+2)}$
$R(s)$, $Y(s)$, and $E(s)$ are the Laplace transforms of $r(t)$, $y(t)$, and $e(t)$, respectively.
If the input $r(t)$ is a unit step function, then

Ques 10 Control Systems
Consider a unity negative feedback control system with forward path gain $G(s)=\frac{K}{(s+1)(s+2)(s+3)}$ as shown.

Ques 11 Control Systems
A satellite attitude control system, as shown below, has a plant with transfer function $G(s)=\frac{1}{s^2}$ cascaded with a compensator $C(s)=\frac{K(s+α)}{s+4}$ where K and α are positive real constants.
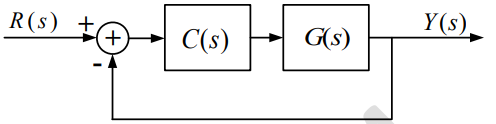
Ques 12 Control Systems
Consider a system S represented in state space as
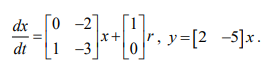
Ques 13 Digital Circuits
For the Boolean function
$F(A,B,C,D)=\Sigma m(0,2,5,7,8,10,12,13,14,15)$,
the essential prime implicants are

Total Unique Visitors