Electronics & Communication Gate Yearwise 

Electronics and Communication Gate 2019 Questions with Answer

Ques 53 GATE 2019

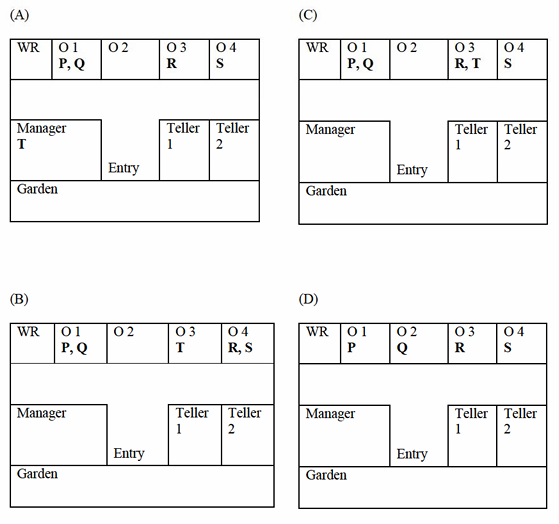
Five people P, Q, R, S and T work in a bank. P and Q don't like each other but have to share an office till T gets a promotion and moves to the big office next to the garden. R, who is currently sharing an office with T wants to move to the adjacent office with S, the handsome new intern. Given the floor plan, what is the current location of Q, R and T?

A

Refer to figure (A)

B

Refer to figure (B)

C

Refer to figure (C)

D

Refer to figure (D)


(c) is the correct answer.

Ques 54 GATE 2019

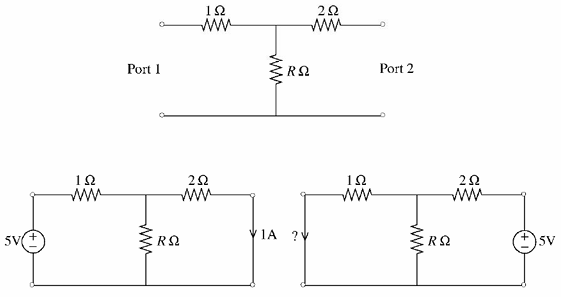
Consider the two-port resistive network shown in the figure. When an excitation of 5 V is applied across Port 1, and Port 2 is shorted, the current through the short circuit at Port 2 is measured to be 1 A (see (a) in the figure). Now, if an excitation of 5 V is applied across Port 2, and Port 1 is shorted (see (b) in the figure), what is the current through the short circuit at Port 1?

A

0.5 A

B

1 A

C

2 A

D

2.5 A


(b) is the correct answer.

Ques 55 GATE 2019

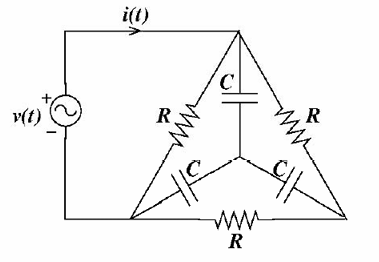
In the circuit shown, if v(t)=2sin(1000t) volts, R=1kΩ and C=1μF, then the steady-state current i(t), in milliamperes (mA), is

A

sin(1000t)+cos(1000t)

B

2sin(1000t)+2cos(1000t)

C

3sin(1000t)+cos(1000t)

D

sin(1000t)+3cos(1000t)


(c) is the correct answer.

Ques 56 GATE 2019

The RC circuit shown below has a variable resistance R(t) given by the following expression: R(t)=R0(1-t/T) for 0≤t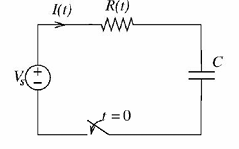0=1 Ω and C=1 F. We are also given that T=3 R0C and the source voltage is Vs=1 V. If the current at time t=0 is 1 A, then the current I(t), in amperes, at time t=T/2 is... (rounded off to 2 decimal places).


(0.25) is the correct answer.

Ques 57 GATE 2019

Let Z be an exponential random variable with mean 1. That is, the cumulative distribution function of Z is given by Fz(x) = 1-e-x if x≥0 and 0 if x<0. Then Pr(Z>2|Z>1) rounded off to two decimal places, is equal to


(0.37) is the correct answer.

Ques 58 GATE 2019

A random variable X takes values -1 and +1 with probabilities 0.2 and 0.8, respectively. It is transmitted across a channel which adds noise N, so that the random variable at the channel output is Y=X+N. The noise N is independent of X, and is uniformly distributed over the interval [-2, 2]. The receiver makes a decision ̂X=-1, if Y≤θ and ̂X=+1, if Y>θ where the threshold θ∈[-1,1] is chosen so as to minimize the probability of error Pr[̂X≠X]. The minimum probability of error, rounded off to 1 decimal place, is


(0.1) is the correct answer.

Ques 59 GATE 2019

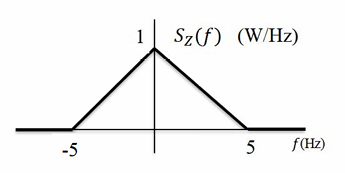
Let a random process Y(t) be described as Y(t)=h(t)*X(t)+Z(t), where X(t) is a white noise process with power spectral density Sx(f)=5 W/Hz. The filter h(t) has a magnitude response given by |H(f)|=0.5 for -5≤f≤5 and zero elsewhere. Z(t) is a stationary random process, uncorrelated with X(t), with power spectral density as shown in the figure. The power in Y(t), in watts, is equal to... W (rounded off to two decimal places).


(17.5) is the correct answer.

Ques 60 GATE 2019

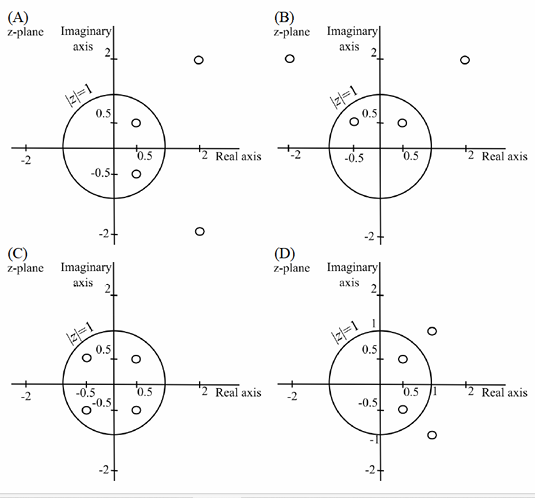
Let H(z) be the z-transform of a real-valued discrete-time signal h[n]. If P(z)=H(z)H(1/z) has a zero at z=1/2 + 1/2j and P(z) has a total of four zeros, which one of the following plots represents all the zeros correctly?

A

Refer to figure (A)

B

Refer to figure (B)

C

Refer to figure (C)

D

Refer to figure (D)


(d) is the correct answer.

Ques 61 GATE 2019

Let Y(s) be the unit-step response of a causal system having a transfer function G(s)=(3-s)/((s+1)(s+3)), that is, Y(s)=G(s)/s. The forced response of the system is

A

u(t)-2e-tu(t)+e-3tu(t)

B

2u(t)-2e-tu(t)+e-3tu(t)

C

2u(t)

D

u(t)


(d) is the correct answer.

Ques 62 GATE 2019

Consider the signal f(t)=1+2cos(πt)+3sin(2πt/3)+4cos(πt/2 + π/4), where t is in seconds. Its fundamental time period, in seconds, is


(12) is the correct answer.

Ques 63 GATE 2019

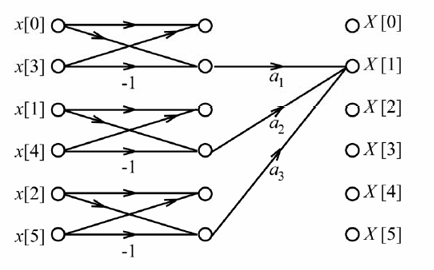
Consider a six-point decimation-in-time Fast Fourier Transform (FFT) algorithm, for which the signal-flow graph corresponding to X[1] is shown in the figure. Let W6=exp(-j2π/6). In the figure, what should be the values of the coefficients a1, a2, a3 in terms of W6 so that X[1] is obtained correctly?

A

a1=-1, a2=W6, a3=W62

B

a1=1, a2=W62, a3=W6

C

a1=1, a2=W6, a3=W62

D

a1=-1, a2=W62, a3=W6


(c) is the correct answer.

Ques 64 GATE 2019

It is desired to find a three-tap causal filter which gives zero signal as an output to an input of the form x[n]=c1exp(-jπn/2)+c2exp(jπn/2) where c1 and c2 are arbitrary real numbers. The desired three-tap filter is given by h[0]=1, h[1]=a, h[2]=b, and h[n]=0 for n<0 or n>2. What are the values of the filter taps a and b if the output is y[n]=0 for all n, when x[n] is as given above?

A

a=1, b=1

B

a=0, b=-1

C

a=-1, b=1

D

a=0, b=1


(d) is the correct answer.

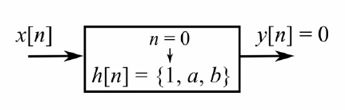
Ques 65 GATE 2019

Let h[n] be a length-7 discrete-time finite impulse response filter, given by h[0]=4, h[1]=3, h[2]=2, h[3]=1, h[-1]=-3, h[-2]=-2, h[-3]=-1, and h[n] is zero for |n|≥4. A length-3 finite impulse response approximation g[n] of h[n] has to be obtained such that E(h,g)=∫-ππ|H(ejω)-G(ejω)|2dω is minimized, where H(ejω) and G(ejω) are the discrete-time Fourier transforms of h[n] and g[n], respectively. For the filter that minimizes E(h,g), the value of 10g[-1]+g[1], rounded off to 2 decimal places, is


(-27) is the correct answer.

Unique Visitor Count

Total Unique Visitors

Loading......

Question Options

Contributed by: