Electronics & Communication Gate Yearwise 

Electronics and Communication Gate 2013 Set-2 Questions with Answer

Ques 53 Gate 2013 SET-2

Let U and V be two independent and identically distributed random variables such that P(U = +1) = P(U = -1) = 1/2. The entropy H(U + V) in bits is

A

3/4

B

1

C

3/2

D

log23


(c) is the correct answer.

Ques 54 Gate 2013 SET-2

Let U and V be two independent zero mean Gaussian random variables of variances 1/4 and 1/9 respectively. The probability P(3V ≥ 2U) is

A

4/9

B

1/2

C

2/3

D

5/9


(b) is the correct answer.

Ques 55 Gate 2013 SET-2

The impulse response of a continuous time system is given by h(t) = δ(t - 1) + δ(t - 3). The value of the step response at t = 2 is

A

0

B

1

C

2

D

3


(b) is the correct answer.

Ques 56 Gate 2013 SET-2

A system is described by the differential equation
d2y/dt2 + 5dy/dt + 6y = x(t).
Let x(t) be a rectangular pulse given by
x(t) = 1, 0 < t < 2
x(t) = 0, otherwise
Assuming that y(0) = 0 and dy/dt = 0 at t = 0, the Laplace transform of y(t) is

A

e-2s/[s(s + 2)(s + 3)]

B

(1 - e-2s)/[s(s + 2)(s + 3)]

C

e-2s/[(s + 2)(s + 3)]

D

(1 - e-2s)/[(s + 2)(s + 3)]


(b) is the correct answer.

Ques 57 GATE 2013 SET-2

For a periodic signal v(t) = 30 sin100t + 10 cos300t + 6 sin(500t + π/4), the fundamental frequency in rad/s is

A

100

B

300

C

500

D

1500


(a) is the correct answer.

Ques 58 GATE 2013 SET-2

A band-limited signal with a maximum frequency of 5 kHz is to be sampled. According to the sampling theorem, the sampling frequency which is not valid is

A

5 kHz

B

12 kHz

C

15 kHz

D

20 kHz


(a) is the correct answer.

Ques 59 GATE 2013 SET-2

Which one of the following statements is NOT TRUE for a continuous time causal and stable LTI system?

A

All the poles of the system must lie on the left side of the jω axis.

B

Zeros of the system can lie anywhere in the s-plane.

C

All the poles must lie within |s| = 1.

D

All the roots of the characteristic equation must be located on the left side of the jω axis.


(c) is the correct answer.

Ques 60 GATE 2013 SET-2

Assuming zero initial condition, the response y(t) of the system given below to a unit step input u(t) is

A

u(t)

B

tu(t)

C

t2/2 u(t)

D

e-tu(t)


(c) is the correct answer.

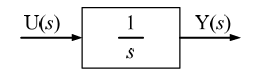
Ques 61 Gate 2013 SET-2

Let g(t) = e-πt2, and h(t) is a filter matched to g(t). If g(t) is applied as input to h(t), then the Fourier transform of the output is

A

e-πf2

B

e-πf2/2

C

e-π|f|

D

e-2πf2


(d) is the correct answer.

Ques 62 Gate 2013 SET-2

Two systems with impulse responses h1(t) and h2(t) are connected in cascade. Then the overall impulse response of the cascaded system is given by

A

product of h1(t) and h2(t)

B

sum of h1(t) and h2(t)

C

convolution of h1(t) and h2(t)

D

subtraction of h2(t) from h1(t)


(c) is the correct answer.

Ques 63 Gate 2013 SET-2

The impulse response of a system is h(t) = tu(t). For an input u(t-1), the output is

A

t2/2 u(t)

B

(t-1)2/2 u(t-1)

C

(t-1)2/2 u(t-1)

D

(t2-1)/2 u(t-1)


(c) is the correct answer.

Ques 64 Gate 2013 SET-2

A system described by a linear, constant coefficient, ordinary, first order differential equation has an exact solution given by y(t) for t > 0, when the forcing function is x(t) and the initial condition is y(0). If one wishes to modify the system so that the solution becomes -2y(t) for t > 0, we need to

A

change the initial condition to -y(0) and the forcing function to 2x(t)

B

change the initial condition to 2y(0) and the forcing function to -x(t)

C

change the initial condition to j2y(0) and the forcing function to j2x(t)

D

change the initial condition to -2y(0) and the forcing function to -2x(t)


(d) is the correct answer.

Ques 65 Gate 2013 SET-2

The DFT of a vector [a b c d] is the vector [α β γ δ]. Consider the product

The DFT of the vector [p q r s] is a scaled version of

A

[α2 β2 γ2 δ2]

B

[α β γ δ]

C

[αβ + βδ + δγ + γα]

D

[α β γ δ]


(a) is the correct answer.

Unique Visitor Count

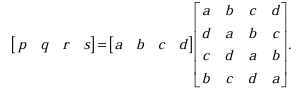
Total Unique Visitors

Loading......

Question Options

Contributed by: