Electronics and Communication Gate 2013 Set-3 Questions with Answer

Ques 27 GATE 2013 SET-3

Statement: You can always give me a ring whenever you need.
Which one of the following is the best inference from the above statement?

Because I have a nice caller tune.

Because I have a better telephone facility.

Because a friend in need is a friend indeed.

Because you need not pay towards the telephone bills when you give me a ring.

Ques 28 GATE 2013 SET-3

In the summer of 2012, in New Delhi, the mean temperature of Monday to Wednesday was 41°C and of Tuesday to Thursday was 43°C. If the temperature on Thursday was 15% higher than that of Monday, then the temperature in °C on Thursday was

Ques 29 GATE 2013 SET-3

The divergence of the vector field A = xa_x + ya_y + za_z is

1/3

(d) is the correct answer.

Ques 30 GATE 2013 SET-3

Consider a vector field A(r). The closed loop line integral ∮A·dl can be expressed as

∬(∇×A)·ds over the closed surface bounded by the loop

∭(∇·A)dv over the closed volume bounded by the loop

∭(∇·A)dv over the open volume bounded by the loop

∬(∇×A)·ds over the open surface bounded by the loop

(d) is the correct answer.

Ques 31 GATE 2013 SET-3

The return loss of a device is found to be 20 dB. The voltage standing wave ratio (VSWR) and magnitude of reflection coefficient are respectively

1.22 and 0.1

0.81 and 0.1

-1.22 and 0.1

2.44 and 0.2

(a) is the correct answer.

Ques 32 GATE 2013 SET-3

A monochromatic plane wave of wavelength λ = 600 μm is propagating in the direction as shown in the figure below.

The angle of incidence θ_i and the expression for E_i are

60° and E₀(â_x - â_z)/√2 e^{-jπ×10⁴(√3x + z)/2} V/m

45° and E₀(â_x + â_z)/√2 e^{-jπ×10⁴√3z/2} V/m

45° and E₀(â_x - â_z)/√2 e^{-jπ×10⁴(√3x + z)/2} V/m

60° and E₀(â_x - â_z)/√2 e^{-jπ×10⁴√3z/2} V/m

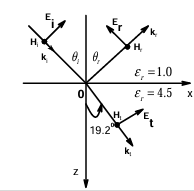
Ques 33 GATE 2013 SET-3

A monochromatic plane wave of wavelength λ = 600 μm is propagating in the direction as shown in the figure below.

The expression for E_r is

E₀(â_x + â_z)/√2 × 0.23 e^{-jπ×10⁴(√3x - z)/2} V/m

E₀(â_x + â_z)/√2 e^{-jπ×10⁴√3z/2} V/m

E₀(â_x + â_z)/√2 × 0.44 e^{-jπ×10⁴(√3x - z)/2} V/m

E₀(â_x + â_z)/√2 e^{-jπ×10⁴(√3x + z)/2} V/m

Ques 34 GATE 2013 SET-3

In IC technology, dry oxidation (using dry oxygen) as compared to wet oxidation (using steam or water vapor) produces

superior quality oxide with a higher growth rate

inferior quality oxide with a higher growth rate

inferior quality oxide with a lower growth rate

superior quality oxide with a lower growth rate

(d) is the correct answer.

Ques 35 GATE 2013 SET-3

In a forward biased pn junction diode, the sequence of events that best describes the mechanism of current flow is

injection, and subsequent diffusion and recombination of minority carriers

injection, and subsequent drift and generation of minority carriers

extraction, and subsequent diffusion and generation of minority carriers

extraction, and subsequent drift and recombination of minority carriers

(a) is the correct answer.

Ques 36 GATE 2013 SET-3

In a MOSFET operating in the saturation region, the channel length modulation effect causes

an increase in the gate-source capacitance

a decrease in the transconductance

a decrease in the unity-gain cutoff frequency

a decrease in the output resistance

(d) is the correct answer.

Ques 37 GATE 2013 SET-3

The small-signal resistance (i.e., dV_B/dI_D) in kΩ offered by the n-channel MOSFET M shown in the figure below, at a bias point of V_B = 2 V is (device data for M: device transconductance parameter k_N = μ_nC_ox(W/L) = 40 μA/V², threshold voltage V_TN = 1 V, and neglect body effect and channel length modulation effects)

12.5

100

(b) is the correct answer.

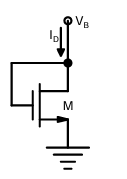
Ques 38 GATE 2013 SET-3

The maximum value of θ until which the approximation sin θ ≈ θ holds to within 10% error is

10°

18°

50°

90°

(b) is the correct answer.

Ques 39 GATE 2013 SET-3

A polynomial f(x) = a₄x⁴ + a₃x³ + a₂x² + a₁x - a₀ with all coefficients positive has

no real roots

no negative real root

odd number of real roots

at least one positive and one negative real root

(d) is the correct answer.

1 2 3 4 5

Total Unique Visitors

Loading......

Electronics & Communication Gate Yearwise

Electronics and Communication Gate 2013 Set-3 Questions with Answer

Question Options

Sign in to ExamPrev