Mathematics GATE CS and IT previous year questions with Answer
Ques 61 GATE 2015 SET-1
Consider the following 2 x 2 matrix A where two elements are unknown and are marked by a and b. The eigenvalues of this matrix are -1 and 7. What are the values of a and b?
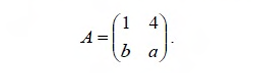
Ques 62 GATE 2014 SET-2
What is the average of all multiples of 10 from 2 to 198?
Ques 63 GATE 2014 SET-2
The value of √(12 + √(12 + √(12 +...))) is
Ques 64 GATE 2014 SET-2
The security system at an IT office is composed of 10 computers of which exactly four are working. To check whether the system is functional, the officials inspect four of the computers picked at random (without replacement). The system is deemed functional if at least three of the four computers inspected are working. Let the probability that the system is deemed functional be denoted by p. Then 100p = _______.
Ques 65 GATE 2014 SET-2
Each of the nine words in the sentence ""The quick brown fox jumps over the lazy dog"" is written on a separate piece of paper. These nine pieces of paper are kept in a box. One of the pieces is drawn at random from the box. The expected length of the word drawn is _______. (The answer should be rounded to one decimal place.)
Ques 66 GATE 2014 SET-2
If the matrix A is such that
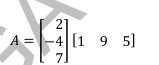
Ques 67 GATE 2014 SET-2
A non-zero polynomial f(x) of degree 3 has roots at x = 1, x = 2 and x = 3. Which one of the following is TRUE?
Ques 68 GATE 2014 SET-2
The probability that a given positive integer lying between 1 and 100 (both inclusive) is NOT divisible by 2, 3 or 5 is _______.
Ques 69 GATE 2014 SET-2
The number of distinct positive integral factors of 2014 is _______.
Ques 70 GATE 2014 SET-2
Consider the following relation on subsets of the set S of integers between 1 and 2014. For two distinct subsets U and V of S we say U < V if the minimum element in the symmetric difference of the two sets is in U. Consider the following two statements:
S1: There is a subset of S that is larger than every other subset.
S2: There is a subset of S that is smaller than every other subset.
Which one of the following is CORRECT?