CS/IT Gate Subject

Aptitude and Reasoning
Engineering Mathematics
C Programming
Data Structure
Design Algorithm Analysis
Operating System
Computer Network
Digital Logic Design
Compiler Design
Database Management System
Theory of Computation

Mathematics GATE CS and IT previous year questions with Answer

Ques 1 Gate 2024 Set-1

Let 𝑓: ℝ → ℝ be a function such that 𝑓(𝑥) = max{𝑥, 𝑥³}, 𝑥 ∈ ℝ , where ℝ is the set of all real numbers. The set of all points where 𝑓(𝑥) is NOT differentiable is

{−1, 1, 2}

{−2, −1, 1}

{0, 1}

{−1, 0, 1}

Ques 2 Gate 2024 Set-1

The product of all eigenvalues of the matrix

−1

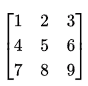
Ques 3 Gate 2024 Set-1

Consider a system that uses 5 bitsfor representing signed integers in 2’s complement format. In this system, two integers 𝐴 and 𝐵 are represented as 𝐴=01010 and 𝐵=11010. Which one of the following operations will result in either an arithmetic overflow or an arithmetic underflow?

𝐴 + 𝐵

𝐴 − 𝐵

𝐵 − 𝐴

2 ∗ 𝐵

Ques 4 Gate 2024 Set-1

Consider a permutation sampled uniformly at random from the set of all permutations of {1, 2, 3, ⋯ , 𝑛} for some 𝑛 ≥ 4. Let 𝑋 be the event that 1 occurs before 2 in the permutation, and 𝑌 the event that 3 occurs before 4. Which one of the following statements is TRUE?

The events 𝑋 and 𝑌 are mutually exclusive

The events 𝑋 and 𝑌 are independent

Either event 𝑋 or 𝑌 must occur

Event 𝑋 is more likely than event 𝑌

Ques 5 Gate 2022

A function y(x) is defined in the interval [0, 1] on the 𝑥-axis as

Which one of the following is the area under the curve for the interval [0, 1] on the 𝑥-axis?

5/6

6/5

13/6

6/13

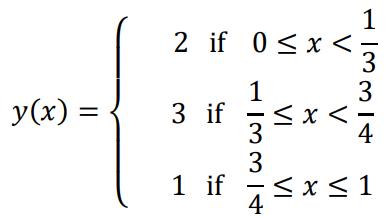
Ques 6 Gate 2022

The value of the following limit is ____________

-0.5 is the correct answer.

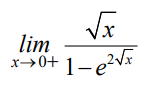
Ques 7 Gate 2022

The number of arrangements of six identical balls in three identical bins is______.

Ques 8 Gate 2022

Consider the following two statements with respect to the matrices A_m×n , B_n×m , C_n×n and D_n×n

Statement 1: tr(AB) = tr(BA)
Statement 2: tr(CD) = tr(DC)
where tr() represents the trace of a matrix. Which one of the following holds?

Statement 1 is correct and Statement 2 is wrong.

Statement 1 is wrong and Statement 2 is correct.

Both Statement 1 and Statement 2 are correct.

Both Statement 1 and Statement 2 are wrong.

Ques 9 GATE 2021 SET-2

If θ is the angle, in degrees, between the longest diagonal of the cube and any one of the edges of the cube, then, cos θ =

1/2

1/√3

1/√2

√3/2

Ques 10 GATE 2021 SET-2

If (x-1/2)² - (x-3/2)² = x + 2, then the value of x is: