CS/IT Gate Subject



Mathematics GATE previous year questions with answer

Ques 92 Gate 2014 Set-1

The base (or radix) of the number system such that the following equation holds is____________.

312/20= 13.1


(a) is the correct answer.

Ques 93 Gate 2014 Set-1

The value of the dot product of the eigenvectors corresponding to any pair of different eigenvalues of a 4-by-4 symmetric positive definite matrix is ____________


(a) is the correct answer.

Ques 94 Gate 2014 Set-1

Consider the following system of equations:

3x + 2y = 1
4x + 7z = 1
x + y + z = 3
x – 2y + 7z = 0

The number of solutions for this system is __________


(a) is the correct answer.

Ques 95 Gate 2014 Set-1

Suppose you break a stick of unit length at a point chosen uniformly at random. Then the expected length of the shorter stick is ________


(a) is the correct answer.

Ques 96 GATE 2014 SET-1

Let the function

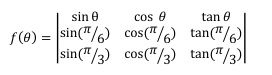
where θ ∈ [π/6, π/3] and f'(θ) denote the derivative of f with respect to θ. Which of the following statements is/are TRUE?
(I) There exists θ ∈ (π/6, π/3) such that f'(θ) = 0
(II) There exists θ ∈ (π/6, π/3) such that f'(θ) ≠ 0

A

I only

B

II only

C

Both I and II

D

Neither I nor II


(c) is the correct answer.

Ques 97 GATE 2014 SET-1

There are 5 bags labeled 1 to 5. All the coins in a given bag have the same weight. Some bags have coins of weight 10 gm, others have coins of weight 11 gm. I pick 1, 2, 4, 8, 16 coins respectively from bags 1 to 5. Their total weight comes out to 323 gm. Then the product of the labels of the bags having 11 gm coins is _______.


(12) is the correct answer.

Ques 98 GATE 2014 SET-1

The function f(x) = x sin x satisfies the following equation: f'(x) + f(x) + t cos x = 0. The value of t is _______.


(-2) is the correct answer.

Ques 99 GATE 2014 SET-1

A function f(x) is continuous in the interval. It is known that f(0) = f(2) = -1 and f(1) = 1. Which one of the following statements must be true?

A

There exists a y in the interval (0, 1) such that f(y) = f(y + 1).

B

For every y in the interval (0, 1), f(y) = f(2 - y).

C

The maximum value of the function in the interval (0, 2) is 1.

D

There exists a y in the interval (0, 1) such that f(y) = -f(2 - y).


(a) is the correct answer.

Ques 100 GATE 2014 SET-1

Four fair six-sided dice are rolled. The probability that the sum of the results being 22 is X/1296. The value of X is _______.


(10) is the correct answer.

Unique Visitor Count

Total Unique Visitors

Loading......

Question Options

Contributed by: