CS/IT Gate Subject



Data Structure GATE CS and IT previous year questions with Answer


Ques 1 Gate 2024 Set-2

Let S1 and S2 be two stacks. S1 has capacity of 4 elements. S2 has capacity of 2 elements. S1 already has 4 elements: 100, 200, 300, and 400, whereas S2 is empty, as shown below.

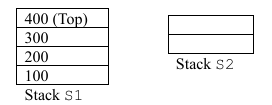
Only the following three operations are available:
PushToS2: Pop the top element from S1 and push it on S2.
PushToS1: Pop the top element from S2 and push it on S1.
GenerateOutput: Pop the top element from S1 and output it to the user.
Note that the pop operation is not allowed on an empty stack and the push operation is not allowed on a full stack.
Which of the following output sequences can be generated by using the above operations?

A

100, 200, 400, 300

B

200, 300, 400, 100

C

400, 200, 100, 300

D

300, 200, 400, 100



Ques 2 Gate 2024 Set-1

Given an integer array of size N, we want to check if the array is sorted (in either ascending or descending order). An algorithm solves this problem by making a single pass through the array and comparing each element of the array only with its adjacent elements. The worst-case time complexity of this algorithm is

A

both Ο(𝑁) and Ξ©(𝑁)

B

Ο(𝑁) but not Ξ©(𝑁)

C

Ξ©(𝑁) but not Ο(𝑁)

D

neither Ο(𝑁) nor Ξ©(𝑁)



Ques 3 Gate 2024 Set-1

In a B+ tree, the requirement of at least half-full (50%) node occupancy is relaxed for which one of the following cases?

A

Only the root node

B

All leaf nodes

C

All internal nodes

D

Only the leftmost leaf node



Ques 4 Gate 2022

Consider the problem of reversing a singly linked list. To take an example, given the linked list below,

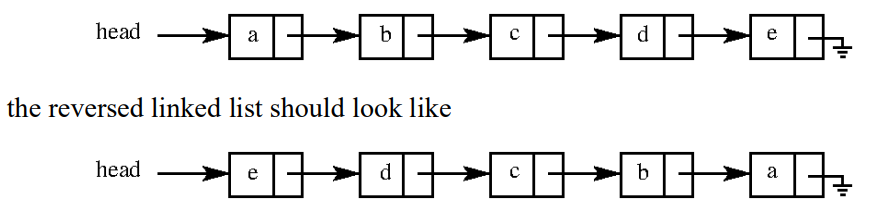
Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O(1) space?

A

The best algorithm for the problem takes θ(n) time in the worst case.

B

The best algorithm for the problem takes θ( nlog n) time in the worst case.

C

The best algorithm for the problem takes θ(n2) time in the worst case.

D

It is not possible to reverse a singly linked list in O(1) space.



Ques 5 Gate 2022

Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?

A

The diagonal entries of A2 are the degrees of the vertices of the graph.

B

If the graph is connected, then none of the entries of An-1+In can be zero.

C

If the sum of all the elements of A is at most 2(n-1), then the graph must be acyclic.

D

If there is at least a 1 in each of A’s rows and columns, then the graph must be connected.



Ques 6 Gate 2022

Consider a simple undirected unweighted graph with at least three vertices. If A is the adjacency matrix of the graph, then the number of 3-cycles in the graph is given by the trace of

A

A3

B

A3 divided by 2

C

A3 divided by 3

D

A3 divided by 6



Ques 7 Gate 2022

Consider a simple undirected graph of 10 vertices. If the graph is disconnected, then the maximum number of edges it can have is ____________.


36 is the correct answer.


Ques 8 Gate 2022

Suppose a binary search tree with 1000 distinct elements is also a complete binary tree. The tree is stored using the array representation of binary heap trees. Assuming that the array indices start with 0, the 3rd largest element of the tree is stored at index_______


509 is the correct answer.


Ques 9 Gate 2020

In a balanced binary search tree with n elements, what is the worst case time complexity of reporting all elements in range [a,b] ? Assume that the number of reported elements is k.

A

Θ(log n)

B

Θ(log(n)+k)

C

Θ(k log n)

D

Θ(n log k)



Ques 10 Gate 2020

Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ VΓ—V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is

A

Θ(∣E∣ + ∣V∣)

B

Θ(∣E∣.∣V∣)

C

Θ(E∣ log ∣V∣)

D

Θ(∣V∣)