CS/IT Gate Subject



Automata GATE CS and IT previous year questions with answer


Ques 1 Gate 2024 Set-2

Let 𝑀 be the 5-state NFA with πœ–-transitions shown in the diagram below.

Which one of the following regular expressions represents the language accepted by 𝑀 ?

A

(00)*⁑ + ⁑1(11)*

B

0*+(1+0(00)*)(11)*

C

(00)* + (1+(00)*)(11)*

D

0+ +1(11)* +0(11)*



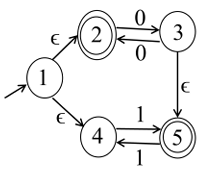
Ques 2 Gate 2023

Which of the following statements is/are CORRECT?

A

The intersection of two recursively enumerable languages is recursively enumerable.

B

The intersection of two recursive languages is recursive.

C

The intersection of two context free languages is context free.

D

The intersection of two regular languages is regular.



a) is correct

The class of recursively enumerable (RE) languages is closed under intersection.
If L1 and L2 are RE languages, then L1 ∩ L2 is also RE.
This can be done by constructing a Turing machine that runs the machines for both L1 and L2 in parallel and accepts if both accept.
For example:
Let L1 = { w | w contains at least one 'a' } and L2 = { w | w contains at least one 'b' }.
Their intersection is L1 ∩ L2 = { w | w contains both 'a' and 'b' }, which is RE.

b) is incorrect

The class of recursive languages is not always closed under intersection.
If L1 and L2 are recursive, their intersection L1 ∩ L2 might not necessarily be recursive because deciding membership in L1 ∩ L2 could require undecidable steps.
For example:
Let L1 = { w | w halts on input 0 } and L2 = { w | w halts on input 1 }.
Their intersection is L1 ∩ L2 = { w | w halts on both input 0 and input 1 }, which is not recursive because the halting problem is undecidable.

c) is incorrect

The class of context-free languages (CFLs) is not closed under intersection.
There exist CFLs L1 and L2 such that their intersection L1 ∩ L2 is not a CFL.
For example:
Let L1 = { an bn cm | n, m β‰₯ 0 } and L2 = { am bn cn | n, m β‰₯ 0 }.
Their intersection is L1 ∩ L2 = { an bn cn | n β‰₯ 0 }, which is not a CFL.

d) is correct

The class of regular languages is closed under intersection.
If L1 and L2 are regular, then L1 ∩ L2 is also regular.
This can be achieved using the product construction of finite automata.
For example:
Let L1 = { w | w starts with 'a' } and L2 = { w | w ends with 'b' }.
Their intersection is L1 ∩ L2 = { w | w starts with 'a' and ends with 'b' }, which is regular.

So, a, c, d is correct option

Ques 3 Gate 2023

Consider the following language L = {w ∈ {0,1}*| w does not contains three or more consecutive 1's}. The number of states in minimal DFA that accepts L is


4 is the correct answer.


Ques 4 Gate 2023

Consider the following grammar:
S β€”> aSb|X
X β€”>aX|Xb|a|b
What can be said about the language generated by grammar?

A

The regular expression for language generated by the grammar is a*(a + b)b*

B

The language generated by the grammar is non-regular

C

The regular expression for language generated by the grammar is a* b*(a + b)

D

The regular expression for language generated by the grammar is (a + b)*



Ques 5 Gate 2022

Which one of the following regular expressions correctly represents the language of the finite automaton given below?

A

(ab*bab*+ ba*aba*)

B

(ab*b)*ab+(ba*a)* ba*

C

(ab*b+ ba*a)* (a*+b*)

D

(ba*a+ ab*b)* (ab*+ba*)



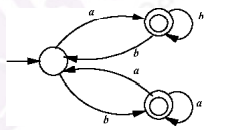
Ques 6 Gate 2022

Which of the following is/are undecidable?

A

Given two Turing machines M1and M2, decide if L(M1)=L(M2).

B

Given a Turing machine M, decide if L(M) is regular.

C

Given a Turing machine M, decide if M accepts all strings.

D

Given a Turing machine M, decide if M takes more than 1073 steps on every string.



Ques 7 Gate 2022

Consider the following languages:

L1 = {ww | w ∈ {a, b}* }
L2 = {anbncn | m, nβ‰₯ 0}
L3 = {ambncn | m, nβ‰₯ 0}
Which of the following statements is/are FALSE?

A

L1 is not context-free but L2 and L3 are deterministic context-free.

B

Neither L1 nor L2 is context-free.

C

L2, L3, and L2 ∩ L3 all are context-free.

D

Neither L1 nor its complement is context-free.



Ques 8 Gate 2022

Which of the following statements is/are TRUE?

A

Every subset of a recursively enumerable language is recursive.

B

If a language L and its complement L are both recursively enumerable, then L must be recursive.

C

The complement of a context-free language must be recursive.

D

If L1 and L2 are regular, then L1∩ L2 must be deterministic context-free.



Ques 9 GATE 2021 SET-1

Suppose that L1 is a regular language and L2 is a context-free language. Which one of the following languages is NOT necessarily context-free?

A

L1∩L2

B

L1β‹…L2

C

L1βˆ’L2

D

L1βˆͺL2



Ques 10 GATE 2021 SET-1

Consider the following statements.

  • S1: The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
  • S2: The sequence of procedure returns corresponds to a postorder traversal of the activation tree.
Which one of the following options is correct?

A

S1 is true and S2 is false

B

S1 is false and S2 is true

C

S1 is true and S2 is true

D

S1 is false and S2 is false