CS/IT Gate Subject



Design Algorithm Analysis GATE previous year questions with answer

Ques 1 Gate 2024 Set-2

The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. The chromatic number of the following graph is _________


(a) is the correct answer.

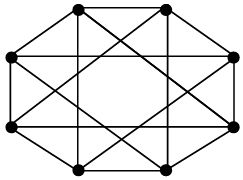
Ques 2 Gate 2024 Set-2

The number of distinct minimum-weight spanning trees of the following graph is _________


(a) is the correct answer.

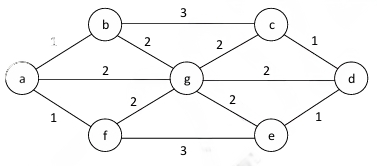
Ques 3 Gate 2022

Consider the following recurrence:

f(1) = 1;
f(2n) = 2f(n) -1, for n≥1;
f(2n+1) = 2f(n) +1, for n≥1;

Then, which of the following statements is/are TRUE?

A

f(2n–1)=2n–1

B

f(2n)=1

C

f(5⋅2n)=2n+1+1

D

f(2n+1)=2n+1


(a,b,c) is the correct answer.

Ques 4 Gate 2022

Which one of the following statements is TRUE for all positive functions f (n) ?

A

f(n2)=θ(f(n)2),when f(n) is a polynomial

B

f(n2)=o(f(n)2)

C

f(n2)=O(f(n)2),when f(n) is a exponential

D

f(n2)=Ω(f(n)2)


(a) is the correct answer.

Ques 5 GATE 2021 SET-1

Let P be an array containing n integers. Let t be the lowest upper bound on the number of comparisons of the array elements, required to find the minimum and maximum values in an arbitrary array of n elements. Which one of the following choices is correct?

A

t>2n−2

B

t>3⌈n/2⌉ and t≤2n−2

C

t>n and t≤3⌈n/2⌉

D

t>⌈log2(n)⌉ and t≤n


(b) is the correct answer.

Ques 6 GATE 2021 SET-1

Consider the following three functions.
f1 = 10n
f2 = nlogn
f3 = n√n
Which one of the following options arranges the functions in the increasing order of asymptotic growth rate?

A

f3,f2,f1

B

f2,f1,f3

C

f1,f2,f3

D

f2,f3,f1


(d) is the correct answer.

Ques 7 Gate 2020

What is the worst case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order ?

A

Θ(n)

B

Θ(nlogn)

C

Θ(n2)

D

Θ(1)


(c) is the correct answer.

Ques 8 Gate 2020

What is the worst case time complexity of inserting n2 elements into an AVL-tree with n elements initially ?

A

Θ(n4)

B

Θ(n2)

C

Θ(n2log(n))

D

Θ(n3)


(c) is the correct answer.

Ques 9 Gate 2020

For parameters a and b, both of which are ω(1), T(n)=T(n1/a)+1, and T(b)=1. Then T(n) is

A

Θ(logalogbn)

B

Θ(logabn)

C

Θ(logblogan)

D

Θ(log2log2n)


(a) is the correct answer.

Ques 10 Gate 2020

The number of permutations of the characters in LILAC so that no character appears in its original position, if the two L’s are indistinguishable, is ________ .


(12 ) is the correct answer.

Unique Visitor Count

Total Unique Visitors

Loading......

Question Options

Contributed by: