Mathematics GATE previous year questions with answer

Ques 66 GATE 2015 SET-2

Let X and Y denote the sets containing 2 and 20 distinct objects respectively and F denote the set of all possible functions defined from X to Y. Let f be randomly chosen from F. The probability of f being one-to-one is _______.

Ques 67 GATE 2015 SET-1

Given Set A = {2, 3, 4, 5} and Set B = {11, 12, 13, 14, 15}, two numbers are randomly selected, one from each set. What is the probability that the sum of the two numbers equals 16?

Ques 68 GATE 2015 SET-1

The probabilities that a student passes in Mathematics, Physics and Chemistry are m, p, and c respectively. Of these subjects, the student has 75% chance of passing in at least one, a 50% chance of passing in at least two and a 40% chance of passing in exactly two. Following relations are drawn in m, p, c:
(I) p + m + c = 27/20
(II) p + m + c = 13/20
(III) (p) x (m) x (c) = 1/10
(A) Only relation I is true.
(B) Only relation II is true.
(C) Relations II and III are true.
(D) Relations I and III are true.

Ques 69 GATE 2015 SET-1

The number of students in a class who have answered correctly, wrongly, or not attempted each question in an exam, are listed in the table below. The marks for each question are also listed. There is no negative or partial marking.

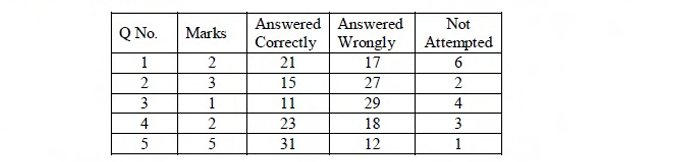
Ques 70 GATE 2015 SET-1

If g(x) = 1 - x and h(x) = x / (x - 1), then g(h(x)) / h(g(x)) is:

Ques 71 GATE 2015 SET-1

lim_{x → ∞} x^1/x is

Ques 72 GATE 2015 SET-1

In the LU decomposition of the matrix

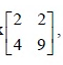
Ques 73 GATE 2015 SET-1

∑_x=1^∞ 1 / (x(x+1)) = _______.

Ques 74 GATE 2015 SET-1

Suppose L = {p, q, r, s, t} is a lattice represented by the following Hasse diagram:

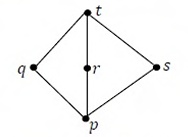
Ques 75 GATE 2015 SET-1

∫_1/π^2/π cos(1/x) / x² dx = _______.