Chemical Engineering Gate 2013 Questions with Answer

Ques 14 GATE 2013

Liquid reactant A decomposes as follows

Ques 15 GATE 2013

In the manufacture of sulphuric acid by the contact process, the catalytic oxidation of SO₂ is carried out in multiple stages mainly to

Ques 16 GATE 2013

Match the reactant-product combination in Group 1 with the unit process in Group 2.
Group 1
(P) propylene - butanol
(Q) cumene - phenol
(R) butane - butadiene
(S) ethylene dichloride - vinyl chloride
Group 2
(1) Pyrolysis
(2) Dehydrogenation
(3) Hydroformylation
(4) Peroxidation

Ques 17 GATE 2013

Identify which of the following statements are FALSE.
(P) Oils with an oleic radical (1 double bond) are more suitable than oils with a linolenic radical (3 double bonds) as film forming vehicles for paints
(Q) Production of synthesis gas from coal and steam is an endothermic process
(R) Use of chlorine for bleaching of wood pulp results in the release of dioxins
(S) In the manufacture of urea from ammonia, the main intermediate product formed is ammonium bicarbonate

Ques 18 GATE 2013

Which of the following statements are TRUE?
P. The eigenvalues of a symmetric matrix are real
Q. The value of the determinant of an orthogonal matrix can only be +1
R. The transpose of a square matrix A has the same eigenvalues as those of A
S. The inverse of an 'n×n' matrix exists if and only if the rank is less than 'n'

Ques 19 GATE 2013

Evaluate ∫ dx/(e^x-1) (Note: C is a constant of integration.)

Ques 20 GATE 2013

The solution of the differential equation dy/dx-y²=0 given y=1 at x=0 is

Ques 21 GATE 2013

The solution of the differential equation d²y/dx²-dy/dx+0.25y=0 , given y=0 at x=0 and dy/dx=1 at x=0 is

Ques 22 GATE 2013

The value of the integral ∫_0.1^0.5 e^-x3dx evaluated by Simpson's rule using 4 subintervals (up to 3 digits after the decimal point) is

Ques 23 GATE 2013

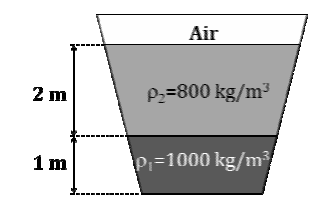
An open tank contains two immiscible liquids of densities (800 kg/m³ and 1000 kg/m³) as shown in the figure. If g=10 m/s², under static conditions, the gauge pressure at the bottom of the tank in Pa is

Ques 24 GATE 2013

The apparent viscosity of a fluid is given by 0.007|dV/dy|^0.3 where (dV/dy) is the velocity gradient. The fluid is

Ques 25 GATE 2013

The mass balance for a fluid with density (ρ) and velocity vector (&vec;v) is

Ques 26 GATE 2013

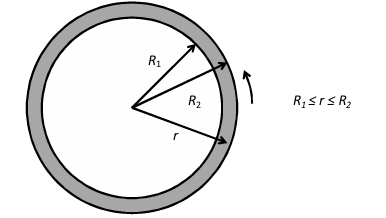
An incompressible Newtonian fluid, filled in an annular gap between two concentric cylinders of radii R₁ and R₂ as shown in the figure, is flowing under steady state conditions. The outer cylinder is rotating with an angular velocity of Ω while the inner cylinder is stationary. Given that (R₂-R₁)«R₁ the profile of the θ-component of the velocity V_θ can be approximated by,