Aerospace Engineering Gate Yearwise 


Aerospace Engineering Gate 2011 Questions with Answer

Ques 53 GATE 2011

An Euler-Bernoulli beam in bending is assumed to satisfy

A

both plane stress as well as plane strain conditions

B

plane strain condition but not plane stress condition

C

plane stress condition but not plane strain condition

D

neither plane strain condition nor plane stress condition


(c) is the correct answer.

Ques 54 GATE 2011

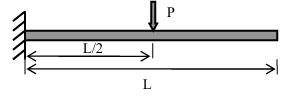
Consider a cantilever beam having length L=1 m, square cross-section (width = depth =0.01 m)
and Young's modulus 50 GPa. The beam is subjected to a transverse load P=1 N at the mid-span
(L/2) at the center of the cross-section. Under the small deformation theory, the transverse
deflection of the beam (in mm) at its free-end is


(2.50) is the correct answer.

Ques 55 GATE 2011

Consider a beam in bending with a solid circular cross-section of 1mm2 which is subjected to a
transverse shear force of 1 N. The shear stress at the center of the cross-section (in N/mm2) is


(1.33) is the correct answer.

Ques 56 GATE 2011

A simply supported slender column of square cross section (width=depth=d) has to be designed
such that it buckles at the same instant as it yields. Length of the column is given to be 1.57 m and
it is made of a material whose Young's modulus is 200 GPa and yield stress is 240 MPa. The
width, d, of the column (in cm) should be


(6.00) is the correct answer.

Ques 57 GATE 2011

A body undergoes deformation under plane strain conditions when subjected to the following
stresses (in MPa): σxx=450, σyy=450, τxy=75, τxz=0, τyz=0 What are the remaining
components of stresses (in MPa) and strains? Assume the material to be isotropic and linear-elastic
with Young's modulus E=200 GPa and Poisson's ratio ν=1/3

A

σzz=0 εxx=0.00225, εyy=0.00225, γxy=0.002, γxz=0, γyz=0

B

σzz=300, εxx=0.001, εyy=0.001, γxy=0.001, γxz=0 γyz=0

C

σzz=300, εxx=0.00225, εyy=0.00225, γxy=0.001, γxz=0 0,7 γyz=0

D

σzz=0, εxx=0.001, εyy=0.001, γxy=0.002, γxε=0, γyz=0


(b) is the correct answer.

Ques 58 GATE 2011

Which of the following Airy's stress functions could satisfy the given boundary conditions,

assuming constant values of σxx=P; σyy=Q and τxy=R along the boundary?

A

φ=Px22+Qy22-Rxy

B

φ=Py22+Qx22+Rxy

C

φ=Py22+Qx22-Rxy

D

φ=Px22+Qy22+Rxy


(c) is the correct answer.

Ques 59 GATE 2011

The partial differential equation (PDE) governing free vibrations of a uniform Euler–Bernoulli beam is given by: EI ∂4w/∂x4 + m ∂2w/∂t2 = 0, where EI is the flexural stiffness, m is the mass per unit length, w(x, t) is the bending displacement, x is the coordinate along the beam length, t is time, and L is the beam length.

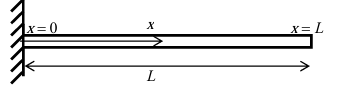
For the cantilever beam shown in the figure, which of the following CANNOT be a possible
boundary condition?

A

w(0,t)=0

B

∂2w∂x2(L,t)=0

C

∂2w∂x2(0,t)=0

D

∂3w∂x3(L,t)=0


(c) is the correct answer.

Ques 60 GATE 2011

A thin-walled (thickness << radius), hollow shaft of length 1 m and mean radius, R = 5 cm has to be designed such that it can transmit a torque, T = 7 kN·m. A survey of different commercially available materials was made and following data was obtained from the suppliers (E: Young’s modulus, τy: yield stress in shear, ρ: density):

Which of the above materials would you choose such that weight of the shaft is minimum?

A

X only

B

Y only

C

Z only

D

X or Y


(b) is the correct answer.

Ques 61 GATE 2011

A thin-walled (thickness << radius), hollow shaft of length 1 m and mean radius, R = 5 cm has to be designed such that it can transmit a torque, T = 7 kN·m. A survey of different commercially available materials was made and following data was obtained from the suppliers (E: Young’s modulus, τy: yield stress in shear, ρ: density):

If you assume a factor of safety of 2, what should be the approximate thickness of such a shaft?

A

0.5 mm

B

1 mm

C

2 mm

D

4 mm


(d) is the correct answer.

Ques 62 GATE 2011

A statically indeterminate frame structure has

A

same number of joint degrees of freedom as the number of equilibrium equations

B

number of joint degrees of freedom greater than the number of equilibrium equations

C

number of joint degrees of freedom less than the number of equilibrium equations

D

) unknown number of joint degrees of freedom, which cannot be solved using laws of mechanics


(b) is the correct answer.

Ques 63 GATE 2011

Consider a simply supported two-dimensional beam

If the beam is converted into a fixed-fixed beam as
then the degree of static indeterminacy will

A

increase by 3

B

increase by 2

C

decrease by 1

D

decrease by 3


(b) is the correct answer.

Ques 64 GATE 2011

Consider a single degree of freedom spring-mass-damper system with mass, damping and stiffness
of m, c and k, respectively. The logarithmic decrement of this system can be calculated using

A

2πc√4mk-c2

B

πc√4mk-c2

C

2πc√mk-c2

D

2πc√mk-4c2


(a) is the correct answer.

Ques 65 GATE 2011

Consider a single degree of freedom spring-mass system of spring stiffness k1 and mass m which
has a natural frequency of 10 rad/s. Consider another single degree of freedom spring-mass system
of spring stiffness k2 and mass m which has a natural frequency of 20 rad/s. The spring stiffness
k2 is equal to

A

k1

B

2k1

C

k14

D

4k1


(d) is the correct answer.

Unique Visitor Count

Total Unique Visitors

Loading......

Question Options

Contributed by: