CS/IT Gate Yearwise
CS/IT Gate 2025 (Set 2)
CS/IT Gate 2024 (Set 1)
CS/IT Gate 2024 (Set 2)
CS/IT Gate 2023
CS/IT Gate 2022
CS/IT Gate 2021 (Set 1)
CS/IT Gate 2021 (Set 2)
CS/IT Gate 2020
CS/IT Gate 2019
CS/IT Gate 2018
CS/IT Gate 2017 (Set 1)
CS/IT Gate 2017 (Set 2)
CS/IT Gate 2016 (Set 1)
CS/IT Gate 2016 (Set 2)
CS/IT Gate 2015 (Set 1)
CS/IT Gate 2015 (Set 2)
CS/IT Gate 2015 (Set 3)
CS/IT Gate 2014 (Set 1)
CS/IT Gate 2014 (Set 2)
CS/IT Gate 2014 (Set 3)
CS and IT Gate 2025 Set-1 Questions with Answer
Ques 1 GATE 2025 SET-1
Let G be any undirected graph with positive edge weights, and T be a minimum spanning tree of G. For any two vertices, u and v, let d1(u,v) and d2(u,v) be the shortest distances between u and v in G and T, respectively. Which ONE of the options is CORRECT for all possible G, T, u and v?
Answer: B — d1(u,v) ≤ d2(u,v)
Explanation:
The tree T is a subgraph of G. Any path that exists in T also exists in G.
Let P be the shortest path between u and v inside T; its length is d2(u,v).
Since P is also a valid path in G, the shortest distance in G cannot be longer than this path.
Therefore:
d1(u,v) ≤ d2(u,v)
Example:
Graph G is a triangle with vertices A, B, C and edge weights:
AB = 1, BC = 1, AC = 3.
A minimum spanning tree T includes edges AB and BC.
In G: shortest A–C path = A–B–C = 1 + 1 = 2 → d1(A,C) = 2
In T: only path A–B–C = 2 → d2(A,C) = 2
Hence, d1 = d2.
Example
Graph G is a triangle with all edges weight 1: AB = BC = AC = 1.
A minimum spanning tree T includes edges AB and BC.
In G: shortest A–C path = AC = 1 → d1(A,C) = 1
In T: only path A–B–C = 1 + 1 = 2 → d2(A,C) = 2
So d1 < d2.
Conclusion:
Removing edges (as when taking a Minimum Spanning Tree) can never make the distance shorter.
Therefore, the correct option is: B — d1(u,v) ≤ d2(u,v).
Ques 2 GATE 2025 SET-1
Consider the following recurrence relation:
T(n)=2T(n-1)+n2n for n>0, T(0)=1.
Which ONE of the following options is CORRECT?
Given: T(n) = 2T(n − 1) + n2n, T(0) = 1
We need to find the asymptotic bound Θ.
Expand the recurrence
T(n) = 2T(n−1) + n2n
= 2(2T(n−2) + (n−1)2n−1) + n2n
= 4T(n−2) + 2(n−1)2n−1 + n2n
= 4T(n−2) + (n−1)2n + n2n
= 4T(n−2) + (2n − 1)2n
T(n) = 2kT(n−k) + Σi=0k−1 2i(n−i)2n−i
When k = n:
T(n) = 2nT(0) + Σi=0n−1 2i(n−i)2n−i
Simplify the terms
Since 2i × 2n−i = 2n,
T(n) = 2n + 2n Σi=0n−1 (n−i)
Σi=0n−1 (n−i) = n + (n−1) + (n−2) + … + 1 = n(n + 1)/2
T(n) = 2n + 2n × (n(n + 1)/2)
T(n) = 2n (1 + n(n + 1)/2)
As n grows large, dominant term ≈ (n² × 2n).
Therefore: T(n) = Θ(n² × 2n)
Final Answer:
Option A: T(n) = Θ(n² × 2n)
Ques 3 GATE 2025 SET-1
The pseudocode of a function fun () is given below:

Explanation:
The code is bubble sort using adjacent swaps whenever A[j] > A[j+1]. For an array of length n = 30 in strict descending order every pair (i,j) with i < j is an inversion. The number of inversions is n(n−1)/2, so total swaps = 30×29/2 = 435.
Ques 4 GATE 2025 SET-1
Let G(V,E) be an undirected and unweighted graph with 100 vertices. Let d(u,v) denote the number of edges in a shortest path between vertices u and v in V. Let the maximum value of d(u,v) u, v∈V such that u≠v, be 30. Let T be any breadth-first-search tree of G. Which ONE of the given options is CORRECT for every such graph G?
Explaination:
- Diameter of G =
max_{u,v} d(u,v)= 30. - Define the radius of G as
rad(G) = min_{x} max_{y} d(x,y). It is always true thatrad(G) ≤ diam(G) ≤ 2 · rad(G). - From
diam(G) = 30we getrad(G) ≥ ⌈30/2⌉ = 15. - For any root
r, a BFS tree T rooted atrhas height equal to the eccentricity ofr, i.e.height(T) = max_{v} d(r,v)which is ≥rad(G). - Therefore for every BFS tree
Twe haveheight(T) ≥ rad(G) ≥ 15. Hence the height is at least 15.
Why other options are wrong (quick examples):
- A (exactly 15): Not guaranteed — if you root at an endpoint of a diameter pair, the BFS tree height can be 30.
- B (exactly 30): Not guaranteed — if you pick a center vertex (when
rad(G)=15), a BFS tree can have height 15. - D (at least 30): False — some BFS trees can have height 15, so "at least 30" is not true for every BFS tree.
Concrete illustrations:
- Take a simple path of 31 vertices (a path graph of length 30). Its diameter is 30. A BFS tree rooted at an endpoint has height 30; a BFS tree rooted at the middle vertex has height 15.
Ques 5 GATE 2025 SET-1
The maximum value of x such that the edge between the nodes B and C is included in every minimum spanning tree of the given graph is ______ (answer in integer)
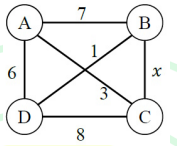
Explanation:
To force the edge BC to appear in every minimum spanning tree (MST), there must be no alternative path from B to C whose largest edge weight is <= x.
If such a path exists, Kruskal's algorithm could connect B and C using that path's edges and skip the direct edge BC.
Examine all simple B–C paths and record the largest edge weight on each path:
- Path B – A – C: edge weights 7 and 1 → largest = 7
- Path B – D – C: edge weights 3 and 8 → largest = 8
- Path B – D – A – C: edge weights 3, 6, 1 → largest = 6
The minimum, over these paths, of the largest-edge value is 6. That means there exists a B–C path whose maximum edge is 6.
For BC to be in every MST we need x < 6 (strictly less than 6), otherwise that path could be used instead of BC.
Since the answer asks for an integer value, the largest integer x satisfying x < 6 is: 5
Ques 6 GATE 2025 SET-1
Which ONE of the following statements is FALSE regarding the symbol table?
Statement A: Symbol table is responsible for keeping track of the scope of variables — This is TRUE. The symbol table manages scope information to determine where variables can be accessed.
Statement B: Symbol table can be implemented using a binary search tree — This is TRUE. Symbol tables can be implemented using various data structures including binary search trees, hash tables, arrays, or linked lists.
Statement C: Symbol table is not required after the parsing phase — This is FALSE. The symbol table is used throughout multiple phases including semantic analysis, intermediate code generation, code optimization, and target code generation, not just during parsing.
Statement D: Symbol table is created during the lexical analysis phase — This is TRUE. The lexical analyzer creates entries for tokens and identifiers when it encounters them during scanning.
✅ Final Answer: Option (C) — Symbol table is not required after the parsing phase.
Reason: The symbol table is used by multiple compilation phases beyond parsing, including semantic analysis, code generation, and optimization phases.
Ques 7 GATE 2025 SET-1
Which ONE of the following techniques used in compiler code optimization uses live variable analysis?
A) Run-time function call management — This involves managing function calls at runtime and does not use live variable analysis.
B) Register assignment to variables — This uses live variable analysis to determine which variables are live at different program points, helping the compiler decide which variables should be allocated to registers and for how long. This is the primary application of live variable analysis.
C) Strength reduction — This optimization replaces expensive operations with cheaper ones (like replacing multiplication by 2 with left shift) and does not require live variable analysis.
D) Constant folding — This optimization evaluates constant expressions at compile time and does not use live variable analysis.
✅ Final Answer: Option (B) — Register assignment to variables.
Reason: Live variable analysis determines which variables are "live" at each program point, which is essential for efficient register allocation and assignment to minimize memory access and optimize performance.
Ques 8 GATE 2025 SET-1
Which of the following statement(s) is/are TRUE while computing First and Follow during top down parsing by a compiler?
Statement A: For a production A→ε, ε will be added to First(A) — This is TRUE. The First set of a non-terminal A includes ε if A can derive the empty string directly.
Statement B: If there is any input right end marker, it will be added to First(S), where S is the start symbol — This is FALSE. The end marker ($) is never added to the First set of any symbol. First sets contain only terminals that can begin strings derived from that symbol.
Statement C: For a production A→ε, ε will be added to Follow(A) — This is FALSE. The fact that A can produce ε does not mean ε is added to Follow(A). Follow sets contain terminals that can appear immediately after a non-terminal, not ε itself.
Statement D: If there is any input right end marker, it will be added to Follow(S), where S is the start symbol — This is TRUE. The end marker ($) is always added to Follow(S) for the start symbol S, indicating the end of input.
✅ Final Answer: Statements A and D are TRUE.
Reason: First sets include ε for productions that derive empty strings, and Follow sets for the start symbol always include the end marker ($). However, end markers are never in First sets, and ε is never in Follow sets.
Ques 9 GATE 2025 SET-1
Refer to the given 3-address code sequence. This code sequence is split into basic blocks. The number of basic blocks is ______ (Answer in integer)
| 1001: | i=1 |
| 1002: | j=1 |
| 1003: | t1=10*i |
| 1004: | t2=t1+j |
| 1005: | t3=8*t2 |
| 1006: | t4=t3-88 |
| 1007: | a[t4]=0.0 |
| 1008: | j=j+1 |
| 1009: | if j<=10 goto 1003 |
| 1010: | i=i+1 |
| 1011: | if i<=10 goto 1002 |
| 1012: | i=1 |
| 1013: | t5=i-1 |
| 1014: | t6=88*t5 |
| 1015: | a[t6]=1.0 |
| 1016: | i=i+1 |
| 1017: | if i<=10 goto 1013 |
To identify basic blocks, we find leaders (starting points) and group consecutive statements until a jump or branch. Leaders include the first statement, targets of jumps, and statements immediately following conditional jumps.
The leaders in this code are at lines 1001, 1002, 1003, 1010, 1012, and 1013. This creates six basic blocks: Block 1 (line 1001), Block 2 (line 1002), Block 3 (lines 1003-1009), Block 4 (lines 1010-1011), Block 5 (line 1012), and Block 6 (lines 1013-1017).
✅ Final Answer: 6
Reason: Each leader starts a new basic block, and consecutive statements without control flow changes belong to the same block.
Ques 10 GATE 2025 SET-1
Identify the ONE CORRECT matching between the OSI layers and their corresponding functionalities as shown.
| OSI Layers | Functionalities |
| (a) Network layer | (I) Packet routing |
| (b) Transport layer | (II) Framing and error handling |
| (c) Datalink layer | (III) Host to host communication |
Network layer (a): Responsible for packet routing between networks, determining the best path for data transmission from source to destination. This matches functionality (I) - Packet routing.
Transport layer (b): Provides host-to-host communication, ensuring end-to-end delivery of data between processes on different hosts. This matches functionality (III) - Host to host communication.
Data link layer (c): Handles framing of data into frames and provides error detection and correction mechanisms for reliable transmission over the physical medium. This matches functionality (II) - Framing and error handling.
Therefore, the correct matching is: Network layer with Packet routing, Transport layer with Host to host communication, and Data link layer with Framing and error handling.
✅ Final Answer: Option (B) — (a)-(I), (b)-(III), (c)-(II).
Reason: Each OSI layer has specific functions: Network layer routes packets, Transport layer provides host-to-host communication, and Data link layer handles framing and error control.
Ques 11 GATE 2025 SET-1
Consider the 3-way handshaking protocol for TCP connection establishment. Let the three packets exchanged during the connection establishment be denoted as P1, P2, and P3, in order. Which of the following option(s) is/are TRUE with respect to TCP header flags that are set in the packets?
Ques 12 GATE 2025 SET-1
A packet with the destination IP address 145.36.109.70 arrives at a router whose routing table is shown. Which interface will the packet be forwarded to?
| Subnet Address | Subnet Mask (in CIDR notation) | Interface |
| 145.36.0.0 | /16 | E1 |
| 145.36.128.0 | /17 | E2 |
| 145.36.64.0 | /18 | E3 |
| 145.36.255.0 | /24 | E4 |
| Default | .. | E5 |
Ques 13 GATE 2025 SET-1
Suppose a 5-bit message is transmitted from a source to a destination through a noisy channel. The probability that a bit of the message gets flipped during transmission is 0.01. Flipping of each bit is independent of one another. The probability that the message is delivered error-free to the destination is ______ (rounded off to three decimal places)
For a message to be delivered error-free, all bits must be transmitted correctly. Since each bit has a probability of 0.99 of being transmitted correctly and bit transmissions are independent, we multiply the probabilities for all 5 bits.
Probability of error-free transmission = (0.99)^5 = 0.9509900499
Rounded to three decimal places, this gives 0.951.
✅ Final Answer: 0.951
Reason: Independent events require multiplication of individual probabilities, and all bits must be correct for error-free delivery.

Total Unique Visitors