CS/IT Gate Yearwise
CS/IT Gate 2025 (Set 2)
CS/IT Gate 2024 (Set 1)
CS/IT Gate 2024 (Set 2)
CS/IT Gate 2023
CS/IT Gate 2022
CS/IT Gate 2021 (Set 1)
CS/IT Gate 2021 (Set 2)
CS/IT Gate 2020
CS/IT Gate 2019
CS/IT Gate 2018
CS/IT Gate 2017 (Set 1)
CS/IT Gate 2017 (Set 2)
CS/IT Gate 2016 (Set 1)
CS/IT Gate 2016 (Set 2)
CS/IT Gate 2015 (Set 1)
CS/IT Gate 2015 (Set 2)
CS/IT Gate 2015 (Set 3)
CS/IT Gate 2014 (Set 1)
CS/IT Gate 2014 (Set 2)
CS/IT Gate 2014 (Set 3)
CS and IT GATE 2014 Set-3 Questions with Answer
Ques 14 Computer Networks
An IP router implementing Classless Inter-domain Routing (CIDR) receives a packet with address 131.23.151.76. The router’s routing table has the following entries:

1 is the correct answer.
Ques 15 Computer Networks
Every host in an IPv4 network has a 1-second resolution real-time clock with battery backup. Each host needs to generate up to 1000 unique identifiers per second. Assume that each host has a globally unique IPv4 address. Design a 50-bit globally unique ID for this purpose. After what period (in seconds) will the identifiers generated by a host wrap around? _________
256 is the correct answer.
Ques 16 Computer Networks
An IP router with a Maximum Transmission Unit (MTU) of 1500 bytes has received an IP packet of size 4404 bytes with an IP header of length 20 bytes. The values of the relevant fields in the header of the third IP fragment generated by the router for this packet are
Ques 17 Computer Organization and Architecture
Consider the following processors (ns stands for nanoseconds). Assume that the pipeline registers have zero latency.
P1: Four-stage pipeline with stage latencies 1 ns, 2 ns, 2 ns, 1 ns.
P2: Four-stage pipeline with stage latencies 1 ns, 1.5 ns, 1.5 ns, 1.5 ns.
P3: Five-stage pipeline with stage latencies 0.5 ns, 1 ns, 1 ns, 0.6 ns, 1 ns.
P4: Five-stage pipeline with stage latencies 0.5 ns, 0.5 ns, 1 ns, 1 ns, 1.1 ns.
Which processor has the highest peak clock frequency?
Ques 18 Computer Organization and Architecture
An instruction pipeline has five stages, namely, instruction fetch (IF), instruction decode and register fetch (ID/RF), instruction execution (EX), memory access (MEM), and register writeback (WB) with stage latencies 1 ns, 2.2 ns, 2 ns, 1 ns, and 0.75 ns, respectively (ns stands for nanoseconds). To gain in terms of frequency, the designers have decided to split the ID/RF stage into three stages (ID, RF1, RF2) each of latency 2.2/3 ns. Also, the EX stage is split into two stages (EX1, EX2) each of latency 1 ns. The new design has a total of eight pipeline stages. A program has 20% branch instructions which execute in the EX stage and produce the next instruction pointer at the end of the EX stage in the old design and at the end of the EX2 stage in the new design. The IF stage stalls after fetching a branch instruction until the next instruction pointer is computed. All instructions other than the branch instruction have an average CPI of one in both the designs. The execution times of this program on the old and the new design are P and Q nanoseconds, respectively. The value of P/Q is _________.
1.50 to 1.60 is the correct answer.
Ques 19 Computer Organization and Architecture
The memory access time is 1 nanosecond for a read operation with a hit in cache, 5 nanoseconds for a read operation with a miss in cache, 2 nanoseconds for a write operation with a hit in cache and 10 nanoseconds for a write operation with a miss in cache. Execution of a sequence of instructions involves 100 instruction fetch operations, 60 memory operand read operations and 40 memory operand write operations. The cache hit-ratio is 0.9. The average memory access time (in nanoseconds) in executing the sequence of instructions is _________.
1.68 to 1.68 is the correct answer.
Ques 20 Data Structures and Algorithms
Let A be a square matrix of size n x n. Consider the following pseudocode. What is the expected output?
C = 100;
for i = 1 to n do
for j = 1 to n do
{
Temp = A[i][j] + C;
A[i][j] = A[j][i];
A[j][i] = Temp;
}
for i = 1 to n do
for j = 1 to n do
output(A[i][j]);
Ques 21 Data Structures and Algorithms
The minimum number of arithmetic operations required to evaluate the polynomial P(X) = X⁵ + 4X³ + 6X + 5 for a given value of X, using only one temporary variable is _________."
7 is the correct answer.
Ques 22 Data Structures and Algorithms
Consider the following rooted tree with the vertex labeled P as the root:
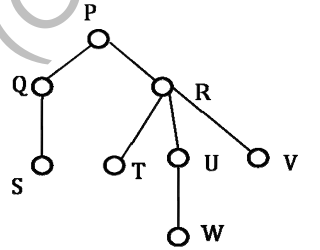
Ques 23 Data Structures and Algorithms
Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.
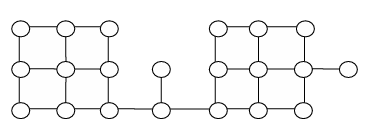
19 is the correct answer.
Ques 24 Data Structures and Algorithms
You have an array of n elements. Suppose you implement quicksort by always choosing the central element of the array as the pivot. Then the tightest upper bound for the worst case performance is
Ques 25 Data Structures and Algorithms
Suppose you want to move from 0 to 100 on the number line. In each step, you either move right by a unit distance or you take a shortcut. A shortcut is simply a pre-specified pair of integers i, j with i < j. Given a shortcut i, j if you are at position i on the number line, you may directly move to j. Suppose T(k) denotes the smallest number of steps needed to move from k to 100. Suppose further that there is at most 1 shortcut involving any number, and in particular from 9 there is a shortcut to 15. Let y and z be such that T(9) = 1 + min(T(y), T(z)). Then the value of the product yz is _________.
150 is the correct answer.
Ques 26 Data Structures and Algorithms
Suppose we have a balanced binary search tree T holding n numbers. We are given two numbers L and H and wish to sum up all the numbers in T that lie between L and H. Suppose there are m such numbers in T. If the tightest upper bound on the time to compute the sum is O(nᵃ logᵇ n + mᶜ logᵈ n), the value of a + 10b + 100c + 1000d is _________.
110 is the correct answer.

Total Unique Visitors