Chemical Engineering Gate Yearwise 


Chemical Engineering Gate 2019 Questions with Answer

Ques 14 GATE 2019

A system of n homogeneous linear equations containing n unknowns will have non-trivial solutions if and only if the determinant of the coefficient matrix is

A

1

B

-1

C

0

D

&infty;


(c) is the correct answer.

Ques 15 GATE 2019

The value of the expression limx → 2π &lvert; x tan x &rvert; is:

A

&infty;

B

0

C

1

D

-1


(a) is the correct answer.

Ques 16 GATE 2019

The product of the eigenvalues of the matrix 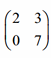is ______ (rounded off to one decimal place).


(14.0) is the correct answer.

Ques 17 GATE 2019

The solution of the ordinary differential equation dy/dx + 3y = 1, subject to the initial condition y=1 at x=0, is

A

(1/3)(1 + 2e-x/3)

B

(1/3)(5 - 2e-x/3)

C

(5/3) - (2/3)e-x/3

D

(1/3)(1 + 2e-3x)


(d) is the correct answer.

Ques 18 GATE 2019

The value of the complex number i-1/2 (where i = √-1) is

A

$\frac{1}{\sqrt{2}}(1-i)$

B

$-\frac{1}{\sqrt{2}}i$

C

$\frac{1}{\sqrt{2}}i$

D

$\frac{1}{\sqrt{2}}(1+i)$


(a) is the correct answer.

Ques 19 GATE 2019

If x, y and z are directions in a Cartesian coordinate system and i, j and k are the respective unit vectors, the directional derivative of the function u(x, y, z) = x2 - 3yz at the point (2,0,-4) in the direction (i + j - 2k)/√6 is ______ (rounded off to two decimal places).


(6.53) is the correct answer.

Ques 20 GATE 2019

Two unbiased dice are thrown. Each dice can show any number between 1 and 6. The probability that the sum of the outcomes of the two dice is divisible by 4 is ______ (rounded off to two decimal places).


(0.25) is the correct answer.

Ques 21 GATE 2019

The Newton-Raphson method is used to determine the root of the equation f(x) = e-x - x. If the initial guess for the root is 0, the estimate of the root after two iterations is ______ (rounded off to three decimal places).


(0.566) is the correct answer.

Ques 22 GATE 2019

For a fully-developed turbulent hydrodynamic boundary layer for flow past a flat plate, the thickness of the boundary layer increases with distance x from the leading edge of the plate, along the free-stream flow direction, as

A

$x^{0.5}$

B

$x^{1.5}$

C

$x^{0.4}$

D

$x^{0.8}$


(d) is the correct answer.

Ques 23 GATE 2019

Consider a cylinder (diameter D and length D), a sphere (diameter D) and a cube (side length D). Which of the following statements concerning the sphericity ( Φ) of the above objects is true:

A

$\Phi_{sphere}>\Phi_{cylinder}>\Phi_{cube}$

B

$\Phi_{sphere}=\Phi_{cylinder}=\Phi_{cube}$

C

$\Phi_{sphere}<\Phi_{cylinder}<\Phi_{cube}$

D

$\Phi_{cylinder}>\Phi_{sphere}=\Phi_{cube}$


(a) is the correct answer.

Ques 24 GATE 2019

For a hydraulic lift with dimensions shown in figure, assuming g = 10 m/s2, the maximum diameter Dleft (in m) that lifts a vehicle of mass 1000 kg using a force of 100 N is ______ (rounded off to two decimal places).


(0.20) is the correct answer.

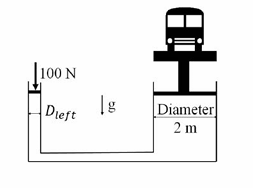
Ques 25 GATE 2019

An incompressible Newtonian fluid flows in a pipe of diameter D1 at volumetric flow rate Q. Fluid with same properties flows in another pipe of diameter D2 = D1/2 at the same flow rate Q. The transition length required for achieving fully-developed flow is l1 for the tube of diameter D1, while it is l2 for the tube of diameter D2. Assuming steady laminar flow in both cases, the ratio l1/l2 is

A

$1/4$

B

1

C

2

D

4


(b) is the correct answer.

Ques 26 GATE 2019

A centrifugal pump is used to pump water (density 1000 kg/m3) from an inlet pressure of 105 Pa to an exit pressure of 2×105 Pa. The exit is at an elevation of 10 m above the pump. The average velocity of the fluid is 10 m/s. The cross-sectional area of the pipes at the pump inlet and outlet is 10-3 m2 and acceleration due to gravity is g = 10 m/s2. Neglecting losses in the system, the power (in Watts) delivered by the pump is ______ (rounded off to the nearest integer).


(2000) is the correct answer.

Unique Visitor Count

Total Unique Visitors

Loading......

Question Options

Contributed by: