Chemical Engineering Gate 2021 Questions with Answer

Ques 14 GATE 2021

Match the common name of chemicals in Group - 1 with their chemical formulae in Group - 2.
Group - 1
P Gypsum
Q Dolomite
R Triple superphosphate
Group - 2
I Ca(H₂PO₄)₂
II CaSO₄.2H₂O
III CaCO₃.MgCO₃
The correct combination is:

Ques 15 GATE 2021

An ordinary differential equation (ODE), dy/dx=2y, with an initial condition y(0)=1, has the analytical solution y=e^2x.
Using Runge-Kutta second order method, numerically integrate the ODE to calculate y at x=0.5 using a step size of h=0.5
If the relative percentage error is defined as, ε=| (y_analytical-y_numerical)/y_analytical | × 100
then the value of ε at x=0.5 is

Ques 16 GATE 2021

The function cos(x) is approximated using Taylor series around x=0 as cos(x)≈1+ax+bx²+cx³+dx⁴. The values of a, b, c and d are

Ques 17 GATE 2021

For the function f(x) = {-x, x<0; x², x≥0} the CORRECT statement(s) is/are

Ques 18 GATE 2021

A source placed at the origin of a circular sample holder (radius r=1 m) emits particles uniformly in all directions. A detector of length l=1 cm has been placed along the perimeter of the sample holder. During an experiment, the detector registers 14 particles.
The total number of particles emitted during the experiment is ________ (round off to nearest integer).

Ques 19 GATE 2021

A, B, C and D are vectors of length 4. A=[a₁ a₂ a₃ a₄]
B=[b₁ b₂ b₃ b₄]
C=[c₁ c₂ c₃ c₄]
D=[d₁ d₂ d₃ d₄]
It is known that B is not a scalar multiple of A. Also, C is linearly independent of A and B. Further, D=3A+2B+C.
The rank of the matrix 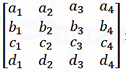is _______.

Ques 20 GATE 2021

Let A be a square matrix of size n×n(n>1). The elements of A={a_ij} are given by

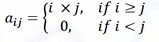
Ques 21 GATE 2021

To solve an algebraic equation f(x)=0, an iterative scheme of the type x_n+1=g(x_n) is proposed, where g(x)=x-(f(x))/(f'(x)). At the solution x=s, g'(s)=0 and g''(s)≠0.
The order of convergence for this iterative scheme near the solution is _______.

Ques 22 GATE 2021

The probability distribution function of a random variable X is shown in the following figure.

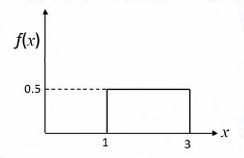
Ques 23 GATE 2021

For the ordinary differential equation d³y/dt³+6d²y/dt²+11dy/dt+6y=1 with initial conditions y(0)=y'(0)=y''(0)=0, the value of lim_t→∞y(t)= _______ (round off to 3 decimal places).

Ques 24 GATE 2021

A batch settling experiment is performed in a long column using a dilute dispersion containing equal number of particles of type A and type B in water (density 1000 kg m^-3) at room temperature.
Type A are spherical particles of diameter 30 μm and density 1100 kg m^-3.
Type B are spherical particles of diameter 10 μm and density 1900 kg m^-3.
Assuming that Stokes' law is valid throughout the duration of the experiment, the settled bed would

Ques 25 GATE 2021

A three-dimensional velocity field is given by V=5x²yi+Cyj-10xyz k, where i, j, k are the unit vectors in x, y, z directions, respectively, describing a cartesian coordinate system. The coefficient C is a constant. If V describes an incompressible fluid flow, the value of C is

Ques 26 GATE 2021

Consider a steady flow of an incompressible, Newtonian fluid through a smooth circular pipe. Let α_laminar and α_turbulent denote the kinetic energy correction factors for laminar and turbulent flow through the pipe, respectively. For turbulent flow through the pipe α_turbulent=((V₀)/‾V)³ (2n²)/((3+n)(3+2n)) Here, ‾V is the average velocity, V₀ is the centerline velocity, and n is a parameter. The ratio of average velocity to the centerline velocity for turbulent flow through the pipe is given by (‾V)/(V₀) = (2n²)/((n+1)(2n+1))
For n=7 the value of α_turbulent/α_laminar is _______ (round off to 2 decimal places).