Chemical Engineering Gate Yearwise 


Chemical Engineering Gate 2010 Questions with Answer

Ques 14 GATE 2010

Match each of the following techniques of polymerization in Group 1, with the corresponding process characteristics in Group II.

GROUP IGROUP II
P. BulkI. Polymer with very high molecular weight can be obtained
Q. SolutionII. Heat removal is crucial but very difficult
R. SuspensionIII. Small amount of undesired low molecular weight polymer is formed
S. EmulsionIV. Polymer concentration in the product stream is low

A

P-1. Q-II. R - III, S - IV

B

P-II, Q-IV, R-III, S-1

C

P-II, Q-III, R-IV, S-1

D

P-II, Q-III. R - I, S - IV


(c) is the correct answer.

Ques 15 GATE 2010

Match each of the polymers in Group I, with the raw material in Group II, from which they are made.
GROUP I
P. Polyester
Q. Polyamide
R. Viscose rayon
S. Epoxy resin
GROUP II
I. Ethylene Glycol
II. Adipic acid
III. Cellulose
IV. Bisphenol

A

P-I.Q-II. R-III, SIV

B

P-II, Q-1, R - III, S - IV

C

P-I.Q- , R - IV, S-III

D

P-III, Q-II, R-IV, S-I


(a) is the correct answer.

Ques 16 GATE 2010

The inverse of the matrix [1 2; 3 4] is

A

[-2 -1; -3/2 -1/2]

B

[-2 3/2; 1 -1/2]

C

[-2 1; 3/2 -1/2]

D

[2 -3/2; -1 1/2]


(d) is the correct answer.

Ques 17 GATE 2010

The Laplace transform of the function shown in the figure below is

A

V(e-at-e-bt)/s

B

V/s(e-bt-e-at)

C

V/s(e-at-e-bt)

D

V/s2(eat-ebs)


(c) is the correct answer.

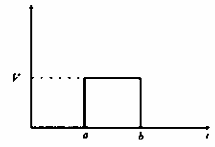
Ques 18 GATE 2010

Given that i=√-1, ii is equal to

A

π/2

B

-1

C

ilni

D

e-π/2


(d) is the correct answer.

Ques 19 GATE 2010

A root of the equation x4-3x+1=0 needs to be found using the Newton-Raphson method. If the initial guess, x0, is taken as 0. then the new estimate, x1, after the first iteration is

A

1/3

B

-1/3

C

3

D

-3


(a) is the correct answer.

Ques 20 GATE 2010

The solution of the differential equation d2y/dt2+2dy/dt+2y=0 with the initial conditions y(0)=0, dy/dt|t=0=-1.

A

-e-tsin t

B

-e-t(1-cos t)

C

-(t+sin t)/2

D

-e-tsin t


(d) is the correct answer.

Ques 21 GATE 2010

If u̅ = y î + xy ĵ and v̅ = x² î + xy² ĵ, then curl(u̅ × v̅) is

A

(2xy²) î − (x + y²) ĵ

B

(xy − x²) î − (y − 3xy) ĵ

C

(2x²y² − 3x³) î − (y³ − 3xy²) k̂

D

(3xy² − x²) î − (y² − 3x²y) ĵ


(b) is the correct answer.

Ques 22 GATE 2010

X and Y are independent random variables. X follows a binomial distribution, with N=5 and p=1/2. Y takes integer values I and 2, with equal probability. Then the probability that X=Y is

A

15/64

B

15/32

C

1/2

D

81/625


(a) is the correct answer.

Ques 23 GATE 2010

A box contains three red and two black balls. Four balls are removed from the box one by one, without replacement. The probability of the ball remaining in the box being red, is

A

609/625

B

3/5

C

2/5

D

81/625


(b) is the correct answer.

Ques 24 GATE 2010

For a function g(x) if g(0)=0 and g'(0)=2, then limx→0 ∫0g(x)(2t/x)dt is equal to

A

∞

B

2

C

0

D

-∞


(b) is the correct answer.

Ques 25 GATE 2010

The stream function in a xy-plane is given below: ψ=(1/2)x2y3. The velocity vector for this stream function is

A

xy3 i0-3/2x2y2 j0

B

3/2x2y2 i0-xy3 j0

C

3/2x2y2 i0+xy3 j0

D

xy3 i0+3/2x2y2 j0


(b) is the correct answer.

Ques 26 GATE 2010

The height of a fluidized bed at incipient fluidization is 0.075 m, and the corresponding voidage is 0.38. If the voidage of the bed increases to 0.5, then the height of the bed would be

A

0.058 m

B

0.061 m

C

0.075 m

D

0.093 m


(d) is the correct answer.

Unique Visitor Count

Total Unique Visitors

Loading......

Question Options

Contributed by: