Mathematics Mechanical previous year questions with answer

Ques 31 Gate 2020 Set-2

Let I be a 100 dimensional identity matrix and E be the set of its distinct (no value appears more than once in E) real eigenvalues. The number of elements in E is ______.

Ques 32 Gate 2020 Set-2

A fair coin is tossed 20 times. The probability that 'head' will appear exactly 4 times in the first ten tosses, and ‘tail’ will appear exactly 4 times in the next ten tosses is ______ (round off to 3 decimal places).

Ques 33 Gate 2019 Set-2

The directional derivative of the function f(x, y) =x²+y² along a line directed from (0,0) to (1,1), evaluated at the point x = 1, y = 1 is

Ques 34 Gate 2019 Set-1

The lengths of a large stock of titanium rods follow a normal distribution with a mean (𝜇) of 440 mm and a standard deviation (𝜎) of 1 mm. What is the percentage of rods whose lengths lie between 438 mm and 441 mm?

Ques 35 Gate 2018 Set-1

Four red balls, four green balls and four blue balls are put in a box. Three balls are pulled out of the box at random one after another without replacement. The probability that all the three balls are red is

Ques 36 GATE 2014 Set-1

Given that the determinant of the matrix is 12, the determinant of the matrix is

Ques 37 GATE 2014 Set-1

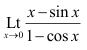is

Ques 38 GATE 2014 Set-1

The argument of the complex number 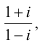where i=√-1, is

Ques 39 GATE 2014 Set-1

The matrix form of the linear system dx/dt=3x-5y and dy/dt=4x+8y is

Ques 40 GATE 2014 Set-1

The question asks to describe the relationship among the three given vectors: ?
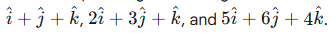