Chemical Engineering > GATE 2018 > Optimization
A person is drowning in sea at location R and the lifeguard is standing at location P. The
beach boundary is straight and horizontal, as shown in the figure.
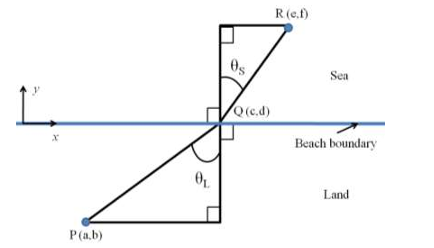The lifeguard runs at a speed of VL and swims at a speed of VS.
In order to reach the drowning person in optimum time, the lifeguard should choose point Q such that __________.
In order to reach the drowning person in optimum time, the lifeguard should choose point Q such that __________.
Explanation
Correct : d
Similar Questions
What is the worst-case time complexity of insertion in an AVL tree?
Which operations on a binary search tree have O(h) complexity?
Compare search complexities of sorted array vs balanced BST.